Exploring Linear Regression

Algorithm · 02 Oct 2019

Linear Regression is the simplest Machine Learning Algorithm and is fundamental to other algorithms such as Polynomial Regression, Logistic Regression and Neural Networks.

Python (Jupyter) Notebook of Linear Regression is on this Github Repository. You can also run the Notebook on Google Collab

What does Linear Regression do?

Let’s consider 2D data on xy plane (x-axis and y-axis). Linear Regression finds the line that best fits the data. The line is in the form of function \(y=f(x)=mx+c\). Linear Regression is similar for nD (n-Dimensional) data as well, but we will focus on 2D data for now.

How to do Linear Regression?

Let’s get with the simplest case of a 2D dataset. I have generated a highly linear dataset (n=200) to work with.

We want a line to best fit the data. How do we define that mathematically?

We would like the difference between the predicted y, (ŷ), and the true value y, given some x, to be as minimum as possible. To summarize, We would like the error of the prediction to be minimum.

[Generally, we minimize the square of the error. This is why linear regression is also called least squares approximation. Also, minimizing squared error and minimizing mean squared error have the same objective.]

The Mean Squared Error of the prediction is given as,

\[E=\frac{1}{n}\sum_{i=0}^{n-1} (\hat{y}_{i} - y_{i})^2\] \[E(m,c)=\frac{1}{n}\sum_{i=0}^{n-1} (mx_{i} + c - y_{i})^2\]

Here, \(E(m,c)\) is an error function with input \(m\) and \(c\). We would like to find the value of \(m\) and \(c\), that minimizers the error value E. We can do this using little calculus and algebra.

The values of \(m\) and \(c\) that minimizes the error function \(E(m,c)\) can be written as,

\[(m^*, c^*) = arg\min_{m, c} E(m,c)\]

This means that, \(m^*\) and \(c^*\) are the values that minimizes the Error.

How do we derive the values of parameters?

We know that the derivative of a function is zero at its minimum. Minimizing the Error function w.r.t. the slope \(m\),

\[\frac{dE}{dm} = \frac{dE(m,c)}{dm} = 0 \tag{1}\]

Simplifying \(E(m,c)\),
\(\begin{align*} E(m,c)&=\frac{1}{n}\sum_{i=0}^{n-1} (mx_{i} + c - y_{i})^2 \\ &=\frac{1}{n}\sum_{i=0}^{n-1} (m^2x_{i}^2 + 2(mx_{i})(c - y_{i}) + (c - y_{i})^2) \\ &=\frac{1}{n}\sum_{i=0}^{n-1} (m^2x_{i}^2 + 2mx_{i}c - 2mx_{i}y_{i} - 2cy_{i} + c^2 + y^2)\\ E(m,c)&=\frac{1}{n}\Big[\sum_{i=0}^{n-1} (m^2x_{i}^2 + 2mx_{i}c - 2mx_{i}y_{i} - 2cy_{i} + y^2) + nc^2\Big] \tag{2} \end{align*}\)

Substituting the value of E from (2) in (1),

\[\begin{align*} \frac{dE(m,c)}{dm} &= \sum_{i=0}^{n-1} (2mx_{i}^2 + 2x_{i}c - 2x_{i}y_{i}) \\ 0 &= 2\sum_{i=0}^{n-1} mx_{i}^2 + 2\sum_{i=0}^{n-1} x_{i}c - 2\sum_{i=0}^{n-1} 2x_{i}y_{i} \\ m &= \frac{\sum_{i=0}^{n-1} x_{i}y_{i} -c\sum_{i=0}^{n-1} x_{i}}{\sum_{i=0}^{n-1} x_{i}^2} \tag{3} \end{align*}\]

Similarly, minimizing the Error function w.r.t. the y-intercept \(c\),

\[\frac{dE}{dc} = \frac{dE(m,c)}{dc} = 0\]

Substituting the value of E from (2),

\[\begin{align*} \frac{dE(m,c)}{dc} &= \sum_{i=0}^{n-1} (2mx_{i}^2 - 2y_{i}) + 2nc \\ 0 &= 2\sum_{i=0}^{n-1} mx_{i} - 2\sum_{i=0}^{n-1} y_{i} + 2nc \\ c &= \frac{\sum_{i=0}^{n-1} y_{i} - m\sum_{i=0}^{n-1} x_{i}}{n} \tag{4} \end{align*}\]

Again, substituting the value of \(c\) in equation (3),

\[\begin{align*} m &= \frac{\sum_{i=0}^{n-1} x_{i}y_{i} -\Big[\frac{\sum_{i=0}^{n-1} y_{i} - m\sum_{i=0}^{n-1} x_{i}}{n}\Big]\sum_{i=0}^{n-1} x_{i}}{\sum_{i=0}^{n-1} x_{i}^2} \\ &= \frac{n\sum_{i=0}^{n-1} x_{i}y_{i} -\sum_{i=0}^{n-1} x_{i}y_{i} + m(\sum_{i=0}^{n-1} x_{i})^2}{n\sum_{i=0}^{n-1} x_{i}^2} \\ m &= \frac{n\sum_{i=0}^{n-1} x_{i}y_{i} -\sum_{i=0}^{n-1} x_{i}y_{i}}{n\sum_{i=0}^{n-1} x_{i}^2 - (\sum_{i=0}^{n-1} x_{i})^2} \tag{5} \end{align*}\]

Using the equation (4) and (5), we can find the line parameters \(m\) and \(c\), given data points \((x_{i}, y_{i})\) for i = 0 … n-1, to best fit the data.

When applied this formula to our dataset, we get:

m = 0.3376, c = 0.7393 and E = 0.00203326

The plot of the line that best fits the data is as follows:

Fig: x vs y plot of data and predicted line

How do we use this Algorithm?

I was confused about this topic when I was first learning this topic. Why don’t we treat x and y equally? What if we find the line \(x=my+c\)? Will it give the same result? What if the data is curvy (non-linear)? These questions helped me understand it better.

Here, we assume that there is one input variable (say x) and one output variable (say y). We learn a function that maps input to the output. This is called as function approximation, i.e. we assume that the data points \((x_{i}, y_{i})\) are drawn from some unknown function \(y_{i} = g(x_{i})\) and we estimate the function \(g(x)\) by \(f(x)\). There may be noise in real-world data, that is why I have made the points slightly scattered. We use the function \(y=f(x)\) to predict the output (y) of some unseen input data (x).

Let us consider an unseen input (say x=0.1). We can predict what would be the value of y at given x. Using the equation of line \(y = mx + c\) where, \(m = 0.3376\) and \(c = 0.7393\) for above dataset, we get,

\[\begin{align*} y &= mx + c \\ y &= 0.3376 \times 0.1 + 0.7393 \\ y &= 0.77306 \end{align*}\]

Plotting the new data (0.1, 0.77306) as predicted by the Linear Regression algorithm.

Fig: x vs y plot of data, predicted line and test point

What are the limits of Linear Regression?

Linear Regression can only learn the straight line (or hyperplane). It can only approximate highly linear functions, or else it will have a very high error. Even in the above example, the data would be fitted better by slightly downward curving line. For curvy function approximation, we will later get into non-linear function approximation. But for now, lets further explore the linear regression.

Linear Regression using Linear Algebra

We can formulate the system of linear equations in terms of matrices (and/or vectors). Equation of line or plane can be represented as below,

\[\textbf{Y} = \textbf{X . W} \tag{6}\]

Here, \(\textbf{X} \in \mathbb{R}^{m\times (n+1)} ;\qquad \textbf{W} \in \mathbb{R}^{(n+1)\times p} ; \qquad\textbf{Y} \in \mathbb{R}^{m\times p}\)
Where, m is the number of data points,
n is the dimension of the input data,
p is the dimension of the output data.

What do the matrices look like?

The Matrix X contains all the input data points, Y contains all the output data points and W contains all the learnable parameters of the Linear Regression.

\[\textbf{X}= \begin{bmatrix} x_{0,0} &x_{0,1} &\cdots &x_{0,n-1} &1 \\ x_{1,0} &x_{1,1} &\cdots &x_{1,n-1} &1 \\ \vdots &\vdots &\ddots &\vdots &\vdots \\ x_{m-1,0} &x_{m-1,1} &\cdots &x_{m-1,n-1} &1 \end{bmatrix}\]

Here, each row is the vector input data with a constant 1. Each column represents data in that axis/dimension of the input dataset.

\[\textbf{W}= \begin{bmatrix} w_{0,0} &w_{0,1} &\cdots &w_{0,p-1} \\ w_{1,0} &w_{1,1} &\cdots &w_{1,p-1} \\ \vdots &\vdots &\ddots &\vdots \\ w_{n,0} &w_{n,1} &\cdots &w_{n,p-1} \end{bmatrix}\]

Here, each row corresponds to the slope of each input dimension and each column represents the slope required to compute each dimension of the output given input. This follows, \(\textbf{W}_{i,j}\) gives us the slope/weight of the i^th input to the j^th output.

\[\textbf{Y}= \begin{bmatrix} y_{0,0} &y_{0,1} &\cdots &y_{0,p-1} \\ y_{1,0} &y_{1,1} &\cdots &y_{1,p-1} \\ \vdots &\vdots &\ddots &\vdots \\ y_{m-1,0} &y_{m-1,1} &\cdots &y_{m-1,p-1} \end{bmatrix}\]

Here, each row represents each output given each input and each column represents the output of the individual dimension of the output. This follows, \(\textbf{Y}_{i,j}\) gives us the output of the i^th input in the j^th dimension of the output.

This looks complicated, but it is the easiest to work with. We must be careful with the dimensions of the matrix and what each element represents in the matrix. This makes our problem highly organized and easy to solve.

What does the matrix look like for our 2D data?

This is how the matrices look like for our previously used 2D dataset.

\(\textbf{X}= \begin{bmatrix} x_{0} &1 \\ x_{1} &1 \\ \vdots &\vdots \\ x_{m-1} &1 \end{bmatrix}\) \(\textbf{W}= \begin{bmatrix} w_{0} \\ w_{1} \end{bmatrix}\) \(\textbf{Y}= \begin{bmatrix} y_{0} \\ y_{1} \\ \vdots \\ y_{m-1} \end{bmatrix}\)

Here, \(\textbf{X} \in \mathbb{R}^{200\times 2} ;\qquad \textbf{W} \in \mathbb{R}^{2\times 1} ;\qquad \textbf{Y} \in \mathbb{R}^{200\times 1}\)
We have one-dimensional input, hence we have two columns (one for 1D input and other for constant of 1s) and with 200 data elements, we have 200 rows. Also, we have 2 elements in the weights corresponding to \(m\) and \(c\) of equation of a line. Finally, we have 200 rows corresponding to the output of 200 input data and 1 column corresponding to the value of \(y\). Hence, we have defined the equation of line \(y=mx+c\) in a different form.

How do we find the matrix W?

This can be solved using simple Linear Algebra. Let’s get back into the equation and solve for W.

\[\begin{align*} \textbf{Y} &= \textbf{X} . \textbf{W} \\ \textbf{X}^{+} . \textbf{Y} &= \textbf{X}^{+} . \textbf{X} . \textbf{W} \\ \textbf{X}^{+} . \textbf{Y} &= \textbf{I} . \textbf{W} \\ \textbf{W} &= \textbf{X}^{+} . \textbf{Y} \tag{7} \end{align*}\]

Here, \(\textbf{X}^{+}\) is the Moore–Penrose pseudoinverse of matrix \(\textbf{X}\) and \(\textbf{I}\) is the identity matrix.

We can easily find the parameters that best fit the line using the equation (7). Let’s try this way of finding the parameters on our previous dataset. We get,

\[\textbf{W}= \begin{bmatrix} 0.3376 \\ 0.7393 \end{bmatrix}\]

These are same values we got by using Least Squares Method (m = 0.3376 & c = 0.7393). This method is easier to understand but it used a different technique to solve for the same parameters.

How do we predict Output for new Input?

Let us consider an unseen input we previously used, i.e. x=0.1. We first construct a matrix with this input of length 1. The input in matrix form is:

\[\textbf{X}= \begin{bmatrix} 0.1 &1 \\ \end{bmatrix}\]

Now finding the output using linear equation (6).

\[\begin{align*} \textbf{Y} &= \textbf{X} . \textbf{W} \\ &= \begin{bmatrix} 0.1 &1 \end{bmatrix} . \begin{bmatrix} 0.3376 \\ 0.7393 \end{bmatrix} \\ &= \begin{bmatrix} 0.77306 \end{bmatrix} \end{align*}\]

This is also the same as what we predicted using equation of a line. We don’t even need to plot the output. It is exactly the same thing, but using different methods.

What happens when the input is multi-dimensional and/or the output is multi-dimensional?
The method is still the same for finding the W matrix as well as predicting new examples. Only the input matrix and the output matrix will be changed. The size of the matrices is directly determined by the dimensions of input and output variables.

Linear Regression using Gradient Descent

We can find the parameters of the line that best fits the data using a recursive search algorithm called gradient descent. Gradient descent is used for searching parameters in various type of machine learning algorithms including Linear Regression, SVM and Neural Network.

Before getting into gradient descent, lets first explore how to find the parameters using a simple search technique. There are various search methods such as random search, grid search, Bayesian optimization, etc. We will look at the random search method for a basic understanding of how parameters can be searched.

Random Search

We can search for the parameters m and b of the linear equation \(y=mx+c\), randomly in some intervals. We know that the value of slope(m) can take value anywhere between \(\pm0\) to \(\pm\infty\). To make the search method simple and bounded in a small range, we search the value of slope using the angle \(\theta\), such that \(m = \tan{\theta}\) where, \(\theta\) = \(0\) to \(\pi\). We can search for m using random theta in this range. Now, for the parameter c, we search between the minimum and maximum values of y. This is because we have all data centered around \(x=0\). In our case, we search for the value of b in range 0.425 to 0.909.

Let’s get started with this search method. We will search randomly for \(10^{5}\) values of \(m\) and \(b\) each in their respective range. We will save the value of m and b for which the error \(E(m,b)\) is minimum.

With this search, we got \(m=0.3335\) and \(c=0.73878\) which is very close to the original value of \(m = 0.3376\) and \(c = 0.7393\). The error of the model with this parameter is \(E=0.002034945\) which is slightly greater than the optimal(minimum) value of \(0.00203326\).

The plot of the line searched using random search method is as follows:

This method is working, but it is very inefficient when the number of parameters grows. It would be great if we could search for the parameters more efficiently, even when the number of parameters of the model increases. This is where the gradient descent search method shines. If we could compute the gradient of the error function with respect to the parameters, we could easily search for the parameters by travelling in the opposite direction of gradient recursively. Let’s see how we can use gradient descent to find the optimal value of parameters of our linear regression method.

Gradient Descent Search

The objective of the gradient descent algorithm is the same as that of Least Squares Regression, i.e. to find the parameters that minimize the error. In the least-squares method, we solved for the parameters using analytical method. Here, we find the parameters using numerical computation and search based method.

Let us begin with the equation of line \(y=f(x)=mx+c\). We want to optimize the parameters m and c to have the minimum error. At first, we need to initialize the parameters to some random values, so that we can calculate the error and further calculate the gradient(required change) of the parameters to reduce the error. The solution is optimal if the gradient is zero, i.e. the error function is minimized.

How do we get the gradient of the parameters?

The gradient should be calculated for current values of parameters using the derivative of error function \(E(m,c)\) with respect to the parameters m and b.

We can compute the outputs for all inputs given current values of m and c according to the equation: \(\hat{y}_{i} = mx_{i} + c\).
The Mean Squared Error for the model can be computed as:

\[E=\frac{1}{2n}\sum_{i=0}^{n-1} (\hat{y}_{i} - y_{i})^2 \tag{8}\]

[This is modified Mean Squared Error. The error is divided by 2 such that the derivative does not have 2 as constant.]

\[E(m,c)=\frac{1}{2n}\sum_{i=0}^{n-1} (mx_{i} + c - y_{i})^2\]

First, lets find the gradient of the Error function with respect to the parameter m,

\[\begin{align*} \frac{dE(m,c)}{dm}&=\frac{1}{2n}\sum_{i=0}^{n-1} 2(mx_{i} + c - y_{i}).x_{i} \\ \Delta m&=\frac{1}{n}\sum_{i=0}^{n-1} (\hat{y}_{i} - y_{i}).x_{i}\\ \Delta m&=\frac{1}{n}\sum_{i=0}^{n-1} \Delta y_{i}.x_{i} \tag{9} \end{align*}\]

Again, lets find the gradient of the Error function with respect to the parameter c,

\[\begin{align*} \frac{dE(m,c)}{dc}&=\frac{1}{2n}\sum_{i=0}^{n-1} 2(mx_{i} + c - y_{i}).x_{i} \\ \Delta c&=\frac{1}{n}\sum_{i=0}^{n-1} (\hat{y}_{i} - y_{i}).1\\ \Delta c&=\frac{1}{n}\sum_{i=0}^{n-1} \Delta y_{i} \tag{10} \end{align*}\]

How do we change the parameters?

We have derived the formula to compute the gradient of the Error function w.r.t the parameters m and c. According to the gradient descent, changing the parameters in the opposite direction of the gradient leads to a decrease in the value of that function (Error function in our case).

We change the parameters of the function as follows:

\[m = m - \alpha.\Delta m \tag{11}\] \[c = c - \alpha.\Delta c \tag{12}\]

Where, \(\alpha < 1\) is the scalar value that limits the step size of the update in each iteration. It is also called the learning rate. We will take \(\alpha = 0.1\) for our model.

If we do this recursively, it will lead to the values of the parameter that minimizes that function. We may not get a gradient equal to zero. In practice, we stop the recursion when the change in the value of error is sufficiently small (eg. below the threshold of \(10^{-4}\)).

Algorithm

Step 1. Initialize \(E = 10^{10}\)(large number) and \(\epsilon=10^{-10}\) (small number)
Step 2. Initialize the parameter \(m\) and \(c\) to some random values.
Step 3. \(E_{prev} = E\)
Step 4. Compute the output \(\hat{y}_{i} = mx_{i} + c\), for i = 0 to n-1
Step 5. Compute the error \(E\) according to equation (8)
Step 6. Compute the gradients \(\Delta m\) and \(\Delta c\) according to equation (9) and (10)
Step 7. Update the parameters \(m\) and \(c\) according to equation (11) and (12)
Step 8. Repeat Step 3 to 7 until \((E_{prev} - E) < \epsilon\)

Visualization

We can visualize this algorithm with our dataset. Gradient Descent moves the line closer and closer to the optimal solution in each iteration. Following is the visualization of gradient descent optimizing the linear function.

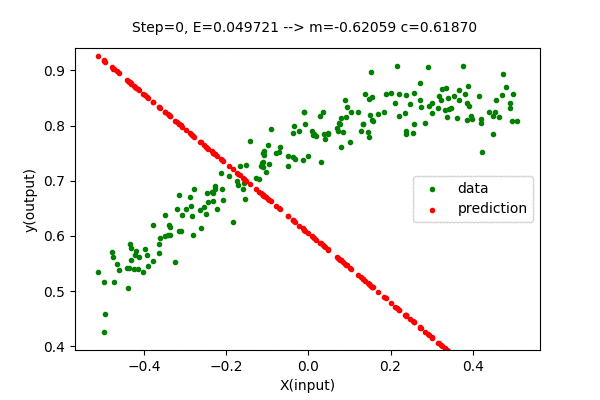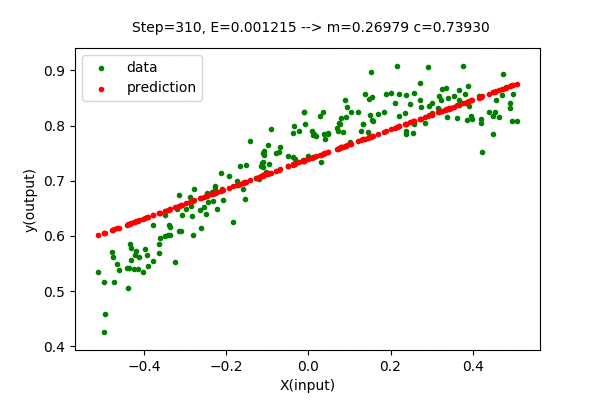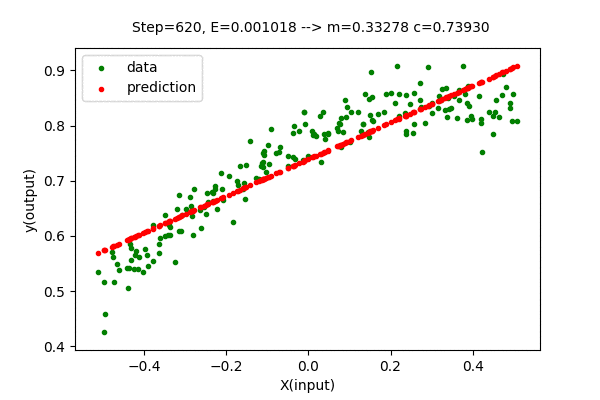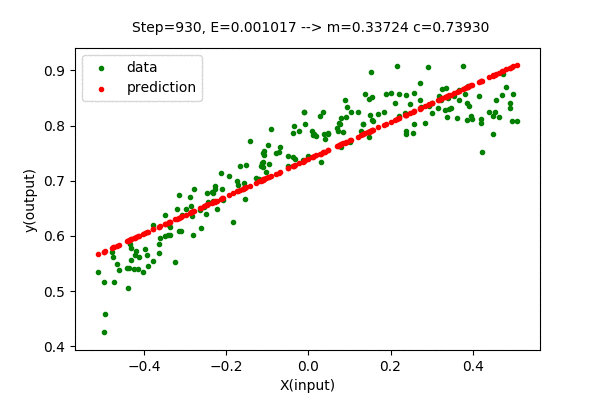
Fig: x vs y plot of data and line predicted by gradient descent

We can see that the error value (E) decreases as parameters change towards the optimal values. After some steps of gradient descent search, the change in error value is negligible, hence it is considered an optimal solution. With this method, we got \(m=0.33724\) and \(c=0.7393\) which is very close to the optimal value of \(m = 0.3376\) and \(c = 0.7393\). The Mean Squared Error(unmodified) of the model with this parameter is \(E=0.00203327\), which is slightly greater than the optimal(minimum) value of \(0.00203326\). But we can close the gap between searched parameter and optimal parameter by increasing the number of updates(iteration).

We can also visualize the Error function \(E(m,c)\) with \(m\) and \(c\) as the input parameters and E as the output of the Error function. The current position(values) of the parameters \(m\) and \(c\) with their error value \(E\) as well as the path taken by the Gradient Descent Algorithm to find the optimal parameters can also be plotted on the same figure.

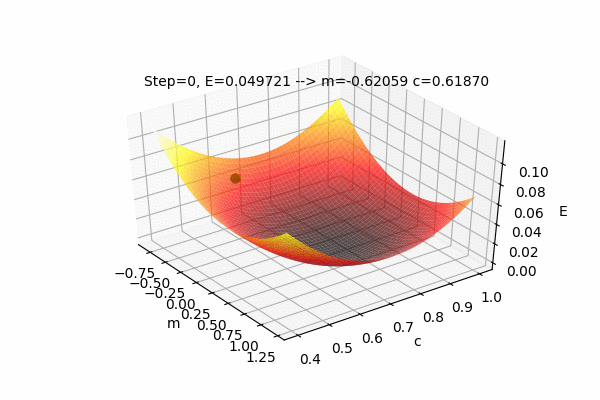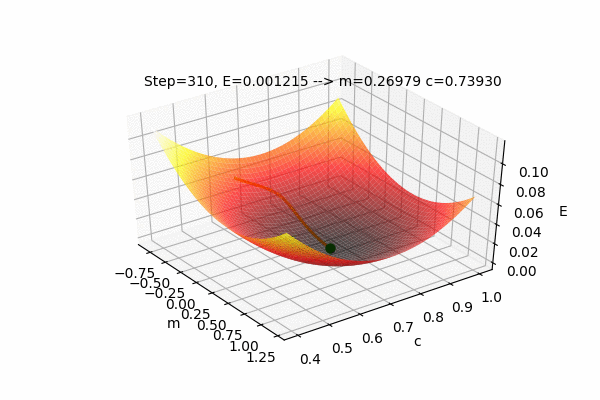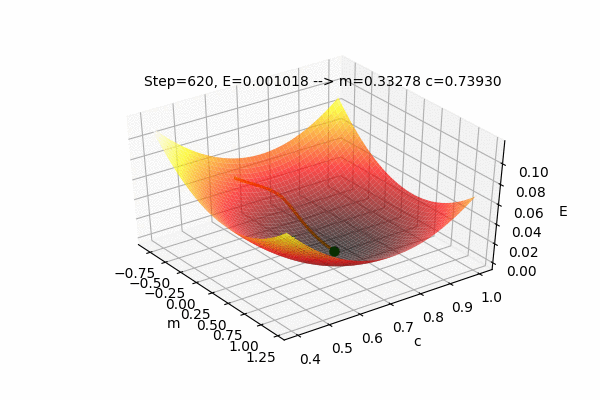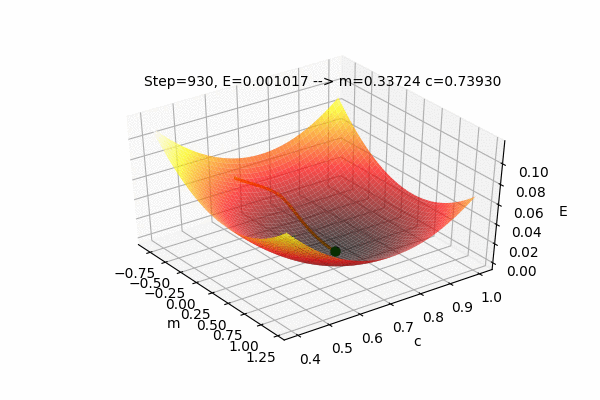
Fig: Error Plot of the Linear Regression optimization

This figure shows the Error function \(E(m,c)\) and the values of parameters updated by the Gradient Descent Algorithm to find the minimum value of the Error, i.e. to minimize the Error function. We can see that the parameters change such that the Error value reaches its minimum. The process of changing the parameters in the opposite direction of their slope, to reach the minimum value of some function is called as Gradient Descent. It is easy to understand if we use the analogy of a ball rolling on some curved surface. The ball always moves towards the lowest height. Similarly, the value of the parameters moves towards the lowest Error.
However, the 3D plot can only show the error function up to 2 parameters. Hence, for models with a large number of parameters, we only plot the error value at different steps. Plot of error values helps us analyze if our model is learning properly. Following is the plot of the error values at various steps of gradient descent in our model. It also shows the minimum error value for our comparison.

Conclusion

We went through the basics of Linear Regression. We have covered a wide variety of topics surrounding Linear Regression. This algorithm is the foundation to understanding concepts such as Model Optimization, Gradient Descent Algorithm and Backpropagation, (Hyper)Parameter Search Techniques, Role of the Error function in Optimization, Curve Fitting, Analytic and Numerical Methods and Visualization. These concepts will be used on many other Machine Learning Algorithms.

If someone is new to this topic, all these things may seem overwhelming. We went through multiple ways of doing the same thing. This will be helpful to clarify the task at hand from a different perspective. Understanding this topic will help us get into other topics such as Polynomial Regression, Logistic Regression, Non-Linear Regression, Neural Networks(Multilayer Perceptron), etc. These topics will be covered in another blog post.

This post may not have covered all the corners of the Linear Regression. There might be several jumps while explaining the topics which may not be clearly understood. After going through the details, there might be even more question and confusion. Please feel free to comment on the post, ask questions or give your feedback.